Ultraviolet Photoelectron Spectroscopy

In photoelectron spectroscopy, electrons are released from the solid by photons. Photon energies between 3 and 100 eV are referred to as UPS. Our source generates He I photons with an energy of 21.2 eV. The photons supply energy to the electrons in the valence band of the solid so that they are excited to states above the vacuum level. These excited electrons with characteristic kinetic energy leave the surface and can then be measured. The surface sensitivity depends on the mean free path of the emitted electrons, as the penetration depth of UV photons is up to 1000 Å, while electrons with energies up to 100 eV have a mean free path of less than 15 Å. This results in an information depth of 2 to 3 atomic layers for UPS. The following applies to the number of electrons that are excited by the UV photons:

D_i and D_f denote the local state densities in the initial and final states. μ fi denotes the matrix element of the dipole transition between the initial and final states. Since the final state densities usually have much less structure than the initial state densities, UPS spectra mainly provide information about the initial state density.

Fig. 3.1 shows a schematic representation of the energy levels during electron excitation by UV photons. A valence electron excited by a photon of energy ħω has a kinetic energy of

E_B is the binding energy of the electron in the solid. The electron is measured in the spectrometer with the kinetic energy

The Fermi levels of the sample E_F,Pr and of the spectrometer E_F,Sp are the same (E_F,Pr = E_F,Sp = E_F), as the sample and the spectrometer are conductively connected. Electrons that are emitted directly from the Fermi level (E_B = E_F) have the maximum kinetic energy:

The position of the Fermi level of the sample is therefore only dependent on the work function of the spectrometer, which can be assumed to be constant, and the photon energy ħω. The low-energy use of the spectrum results in the minimum kinetic energy

From (3.5) and (3.6) we obtain the following for the entire width of the spectrum

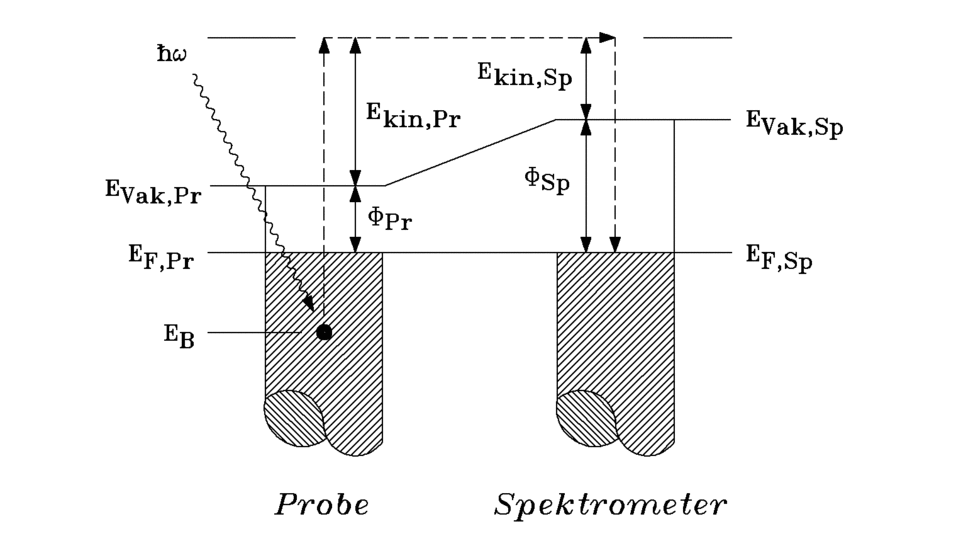
From the width of the measured spectrum and the known photon energy of 21.2 eV, the work function of the sample can be calculated according to (3.7). It is given by the low-energy use of the spectra if the kinetic energy is used as the scale and the Fermi level is set to the photon energy of 21.2 eV. The spectra are calculated as a function of the binding energy E_B which is obtained by subtracting the kinetic energy from the photon energy of 21.2 eV.